
First let $F(x) = x^5$, and let $G(x) = \sin x$. Integrating $f$ by integration by parts would be very tedious, so we will use the method of tabular integration.
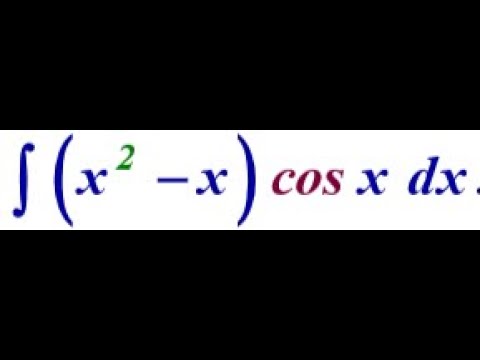
Successively integrate $G(x)$ the same amount of times.Ĭonstruct the integral by taking the product of $F(x)$ and the first integral of $G(x)$, then add the product of $F'(x)$ times the second integral of $G(x)$, then add the product of $F''(x)$ times the third integral of $G(x)$, etc…įor example, consider the function $f(x) = x^5 \sin x$.

Denote the other function in the product by $G(x)$.Ĭreate a table of $F(x)$ and $G(x)$, and successively differentiate $F(x)$ until you reach $0$. In the product comprising the function $f$, identify the polynomial and denote it $F(x)$. The second type is when neither of the factors of $f(x)$ when differentiated multiple times goes to $0$. The first type is when one of the factors of $f(x)$ when differentiated multiple times goes to $0$. tax calculation by invoking the calculateTaxes method in the boot method of. There are two types of Tabular Integration. The Cashier migrations will add several columns to your users table as well.

Tabular integration can be used anytime you need to do integration by parts. Tabular integration is a special technique for integration by parts that can be applied to certain functions in the form $f(x) = g(x)h(x)$ where one of $g(x)$ or $h(x)$ is can be differentiated multiple times with ease, while the other function can be integrated multiple times with ease. In this video we use tabular integration to take care of 4 different integrals.


 0 kommentar(er)
0 kommentar(er)
